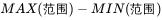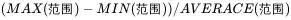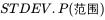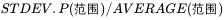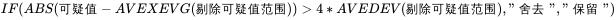涉及到几个手段,分别是:
1.14d检验法
1.2Q检验法
1.3Grubbs检验法
1.4偏态-峰态数据分布正态性检验法
1.5相对极差
1.6STD、RSD
说明:本文公式均为Excel公式,那种大计算公式懒得敲。
对于以上6种手段,其中1-3为离群值的剔除,4也可以做离群值的剔除,详见GB/T 4883-2008偏度-峰度检验法,5-6为整体离散度的一个判断。
图片来自百度,侵删。
离散程度,英文名Measures of Dispersion,是指通过随机地观测变量各个取值之间的差异程度,用来衡量风险大小的指标。
定义来自百度百科。
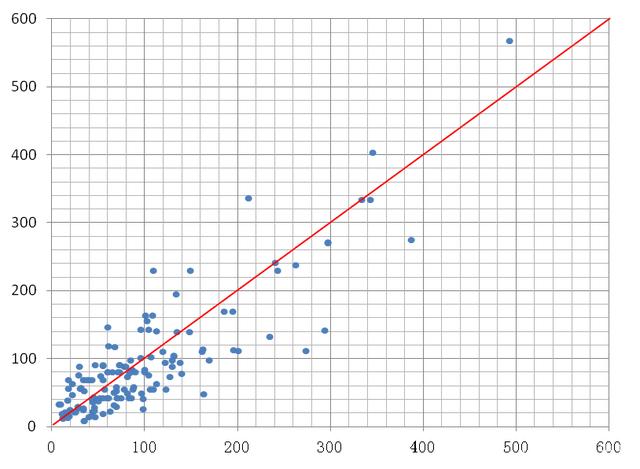
2.1相对极差:
示意图2.1
极差:
对比上图可以看得出来,极差做的就是离散的判断,最基本的计算,所以也叫做全距。
相对极差:
对比上图可以看得出来,引入平均值后,对于相同极差的数据也能够体现出不同的离散度。
但是相对极差不如极差显著。
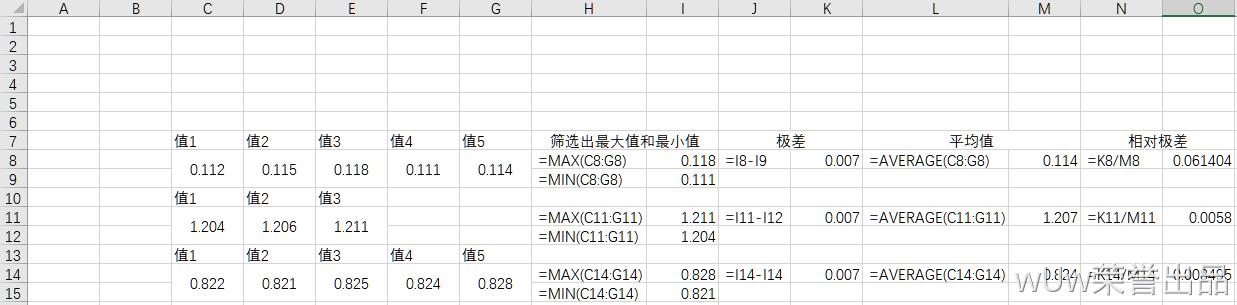
2.2STD、RSD:
示意图2.2
STD:
对比示意图2.2可以看出来,两组数据的离散是一致的,但是两组数据实际并不在一个范畴中,一个属于1以下,一个属于10以上。标准偏差是每个值与平均值比较,因为乘方的关系会扩大这种差异,对于1、2、3、4、5和1、2、2、5、5这种数据,极差是无法处理的,标准偏差就可以明确的给出离散程度的区别。
可以看下面这个示例:
示例图2.2
RSD:
对比示意图2.2可以看得出来,相对标准偏差体现出了两组范畴不同的数据的差别,同样也因为这个平均值,对于10.112和0.112这两组数据就明显体现出精密度的差别了,一个是五位有效数字一个是三位有效数字,同样波动下,显然五位有效数字这组精密度更好。
上面的方法做了离散度的判断,那么具体有哪些值离群了呢?是否可以非主观的去判断离群值从而方便查找原因和数据处理呢?
有。
3.14d检验法:很简单的小方法,问题也不少,先说计算。
示意图3.1
4d检验法
适用于10个数据以上的处理,如果数据量在5~10,可以酌情使用2.5d,问题是数据量不够的时候(