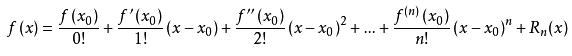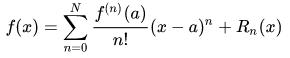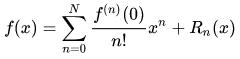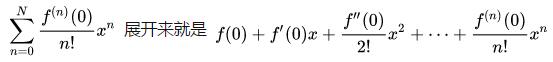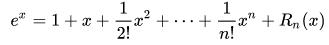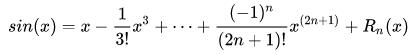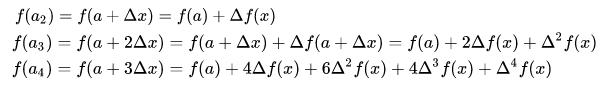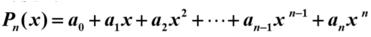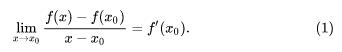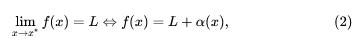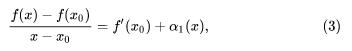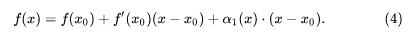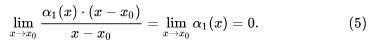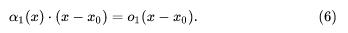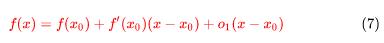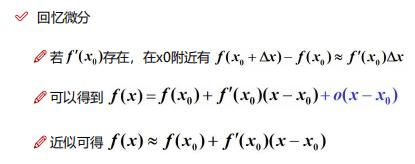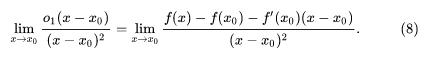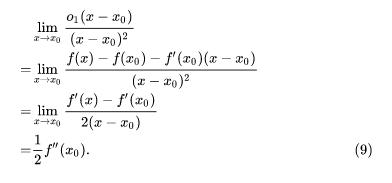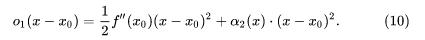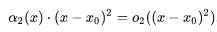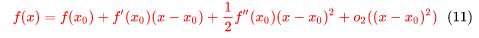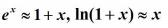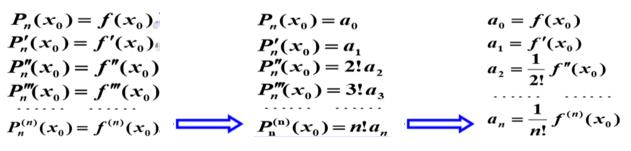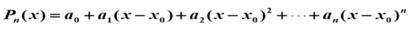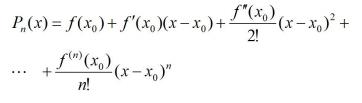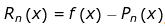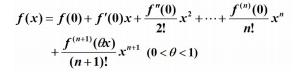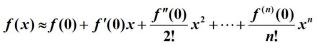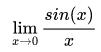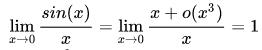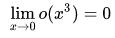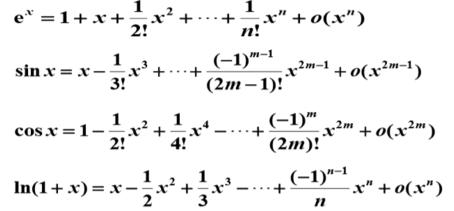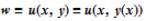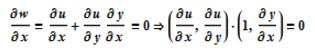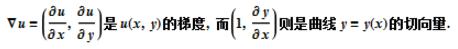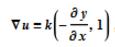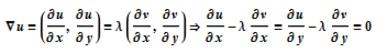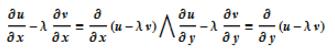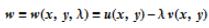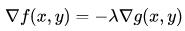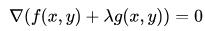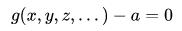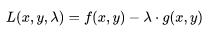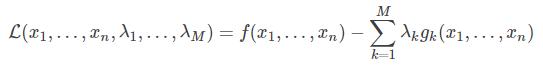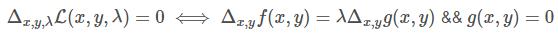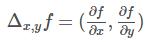泰勒公式,也称泰勒展开式,是用在一个函数在某点的信息,描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,泰勒公式可以利用这些导数值来做系数,构建一个多项式近似函数,求得在这一点的邻域中的值。
泰勒公式用一句话描述:就是用多项式函数去逼近光滑复杂函数,以直代曲。
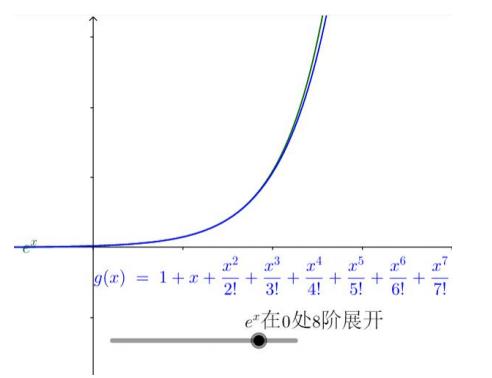
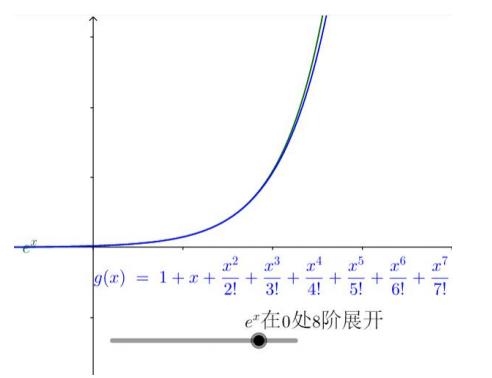
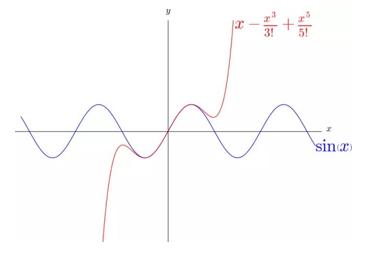
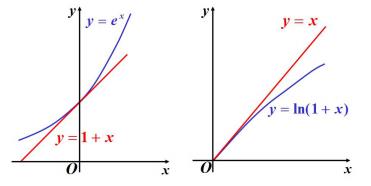
先来感受一下泰勒公式的逼近效果:
泰勒公式的维基百科定义:设 n 是一个正整数,如果定义在一个包含 a 的区间上的函数 f 在 a 点处 n 1 次可导,那么对于这个区间上的任意 x 都有:
其中的多项式称为函数在 a 处的泰勒展开式,Rn(x) 是泰勒公式的余项且是 (x-a)n 的高阶无穷小
这里的余项即为误差,因为使用多项式函数在某点展开,逼近给定函数,最后肯定会有一丢丢的误差,我们称之为余项。
泰勒公式的定义看起来高端大气。但如果 a=0 的话,就是麦克劳伦公式,即:
这个就是我们下面讨论的,可以认为麦克劳伦公式和泰勒公式等价。
泰勒公式的作用就是用一个多项式函数去逼近一个给定的函数(即尽量使多项式函数图像拟合给定的函数图像),注意,逼近的时候一定是从函数图像上的某个点展开。如果是一个非常复杂函数,想求其某点的值,直接求无法实现,这时候就可以使用泰勒公式取近似的求该值,这是泰勒公式的应用之一,泰勒公式在机器学习中主要应用于梯度迭代。
不过这里我们首先看看多项式函数图像特点及其如何逼近给定函数。
初等数学已经了解到一些函数如:ex,sinx,cosx,arctanx,lgx….的一些重要性质,但是初等数学不曾回答怎样来计算他们,下面我们慢慢学习。
首先,我们看一下泰勒展示式:
其中 f(0), f (0)/2! 这些都是常数,我们暂时不管,先看看其中最基础的组成部分,幂函数有什么特点。
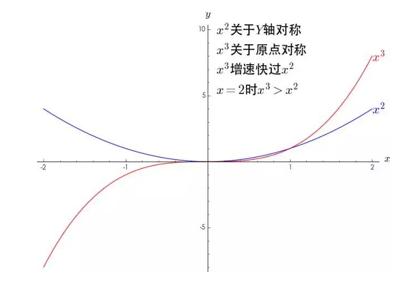
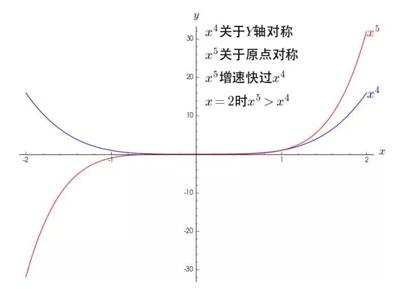
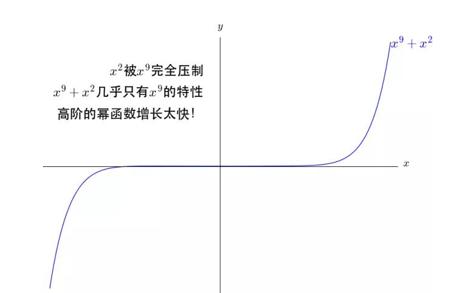
可以看到,幂函数其实只有两种形态,一种是关于 Y 轴对称,一种是关于原点对称,并且指数越大,增长速度越大。
那幂函数组成的多项式函数有什么特点呢?
我们发现:如果把9次的和2次的直接放在一起,那2次的都不用玩了。
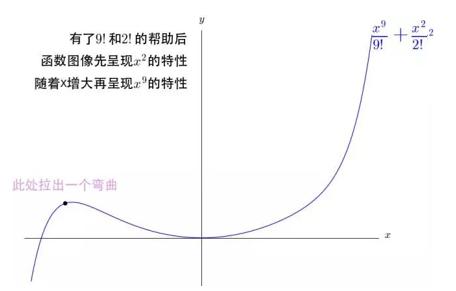
但是开始的时候,应该是2次的效果更好,之后才慢慢轮到9次,可是如何才能让 x2 和 x9 的图像特性能结合起来呢?
所以说,通过改变系数,多项式可以像钢丝一样弯成任意的函数曲线。
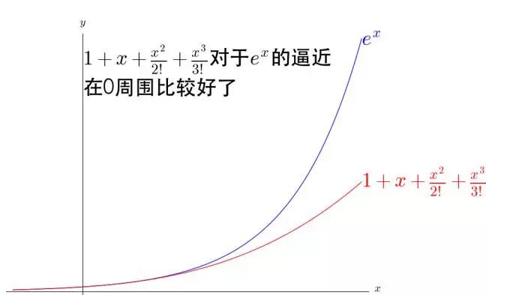
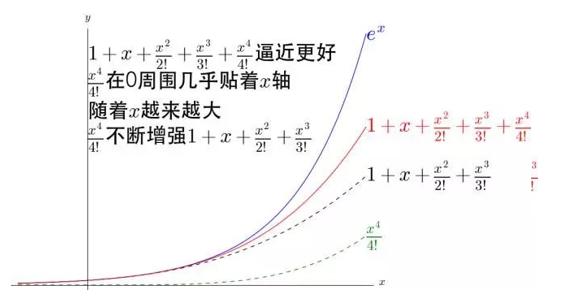
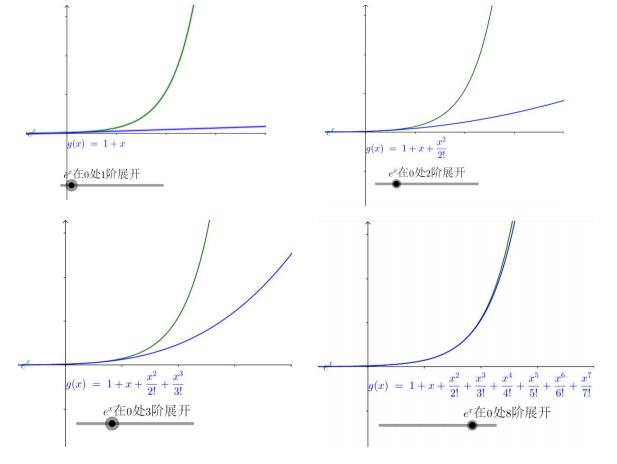
ex 是麦克劳伦展示形式上最简单的函数,有 e 就是这么任性。下面看一下 ex 的多项式展示式:
增加一个 1/4!*x4 看看。
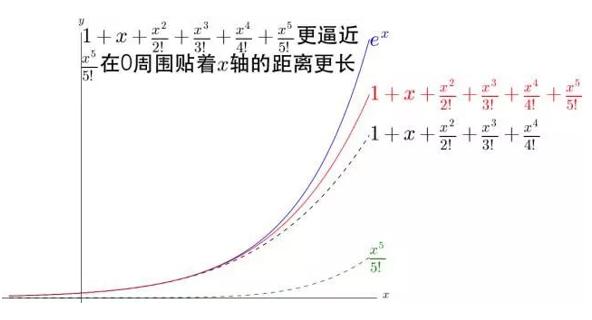
增加一个 1/5!*x5 看看。
可以看出, 1/n!*xn 不断的弯曲着那根多项式形成的铁丝去逼近 ex,并且 n 越大,其作用的区域距离 0 越远。
连起来看,如下:
sin(x) 是周期函数,有非常多的弯曲,难以想象可以用多项式进行逼近。
下面看一下 sin(x) 的多项式展示式。
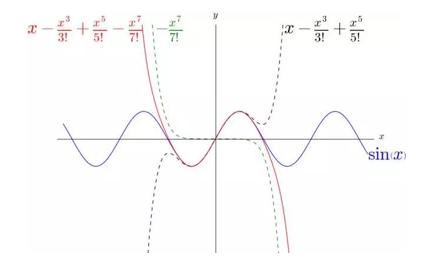
同样,我们再增加一个 1/7!*x7 试试。
可以看到 1/7!*x7 在适当的位置,改变了x – 1/3!*x3 1/5!*x5 的弯曲方向,最终让 x – 1/3!*x3 1/5!*x5 – 1/7!*x7 更好的逼近 sin(x)。
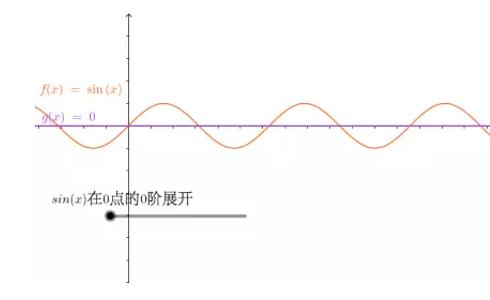
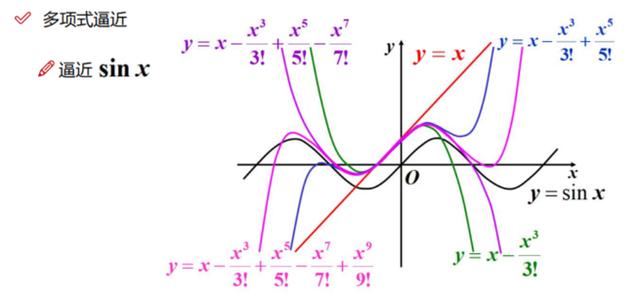
下面看看 sin(x)的泰勒展示:
从上图中每次不同程度的函数逼近可以看出:对于精确度要求较高且需要估计误差的时候,必须用高次多项式来近似表达函数,同时给出误差公式。以上就是利用多项式函数去逼近给定函数的一个过程。
是根据“以直代曲,化整为零”的数学思想,产生了泰勒公式。
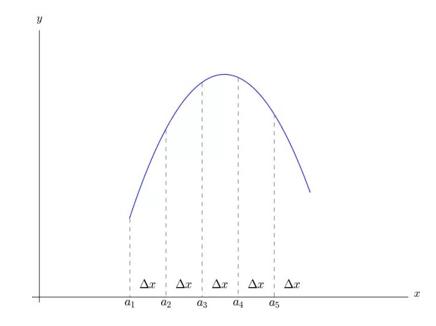
如上图,把曲线等分为 n 份,分别为 a1, a2, …. an,令 a1 = a, a2 = a Δx, … xn = a (n-1)Δx。我们可以退出 (Δ2, Δ3 可以认为是二阶,三阶微分,其准确的数学用于是差分,和微分相比,一个是有限量,一个是极限量):
也就是说, f(x) 全部可以由 a 和 Δx 决定,这个就是泰勒公式提出的基本思想。据此的思想,加上极限 Δx – 0,就可以推出泰勒公式。
注意:为什么泰勒公式选择多项式函数去近似表达给定的函数?
首先,我们看如下多项式:
其实多项式是最简单的一类初等函数。关于多项式,由于它本身的运算仅是有限项加减法和乘法,所以在数值计算方面,多项式是人们乐于使用的工具。因此我们经常用多项式来近似表达函数。这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。
下面我们推导一下其一阶泰勒公式,我们首先从一阶导数着手,假设 f(x) 在 x0 处有一阶导数,那么根据定义,就有:
现在先回顾一下关于函数极限的一个结论:
其中,α(x) 是该极限过程下的某个无穷小,即: α(x) – 0(x -x*),利用这个结论,可以将(1)改写为:
其中 α1(x) – 0(x -x0),再进一步变形,就可以得到:
注意到(4)末尾那一项,很清楚,它是 (x – x0) 的高阶无穷小,这是因为:
于是,我们可以直接将它记作:
这样的话,(4)式就可以进一步改写为:
这就是一阶泰勒公式,老师的PPT如下:
那么如何得到二阶呢?
先比较一下二阶泰勒和一阶泰勒形式上的差别。他们前两项都是一样的,只不过二阶的又多出一项。注意到,高阶无穷小的记号实际上是一个“收纳筐”,它里面装着很多隐藏着的东西。如此,我们猜测,二阶泰勒多出来的这一项,一定是从一阶泰勒那个高阶无穷小中“分析”出来的。
这启发我们来考虑这样一个极限:
这是 一个 0/0 的极限,要求解它可以考虑使用洛必达。但是,请注意,我们现在只有 f(x) 在 x0 一点一阶可导的条件,这还不足以让我们使用洛必达。不过,这并没有太大困难,只要加强条件就行,比如:我们让 f(x) 在 x0 处二阶可导,这样的话,就不仅保证了 f (xo) 存在,还同时保证了 f(x) 在 x0 某邻域内一阶可导,这就满足了洛必达的使用条件。
好了,下面开始洛必达!
现在,我们又利用(2)的结论,将这个极限改写为:
基于同一理由:
我们将它代入(10)并连同(10)一起带回(7),就将得到:
这就是二阶泰勒公式!
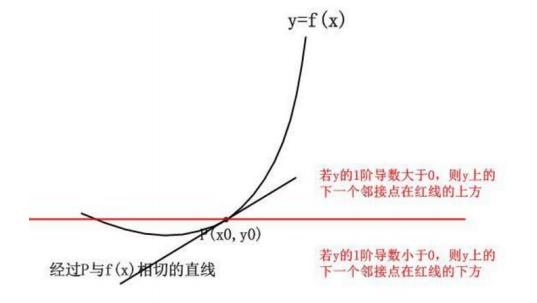
下面看一下以直代曲,当 |x| 很小的时候:
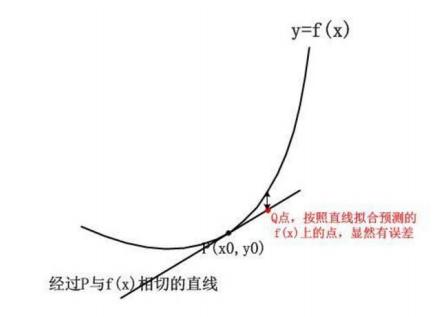
这就相当于,在求一阶导数,求 f(x) 在某一点的切线,这个从函数整体来看,只能表示出下一个点上,函数的整体走势是上升还是下降。
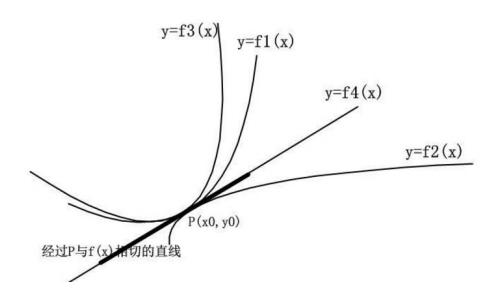
但是我们多画几个函数,就会发现只使用一阶导数看起来有点不准,它只帮我们定位了下一个点是上升还是下降,对之后的趋势就很难把控了。
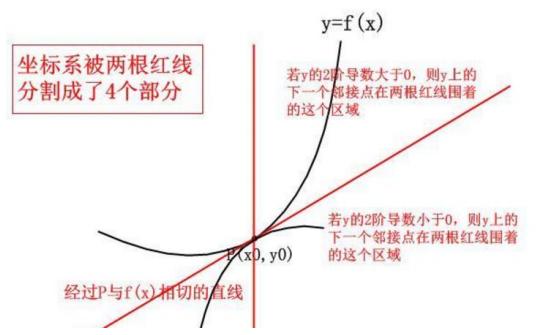
如何做的更准确一些呢? 我们如果把二阶导利用上呢?
更形象一点:
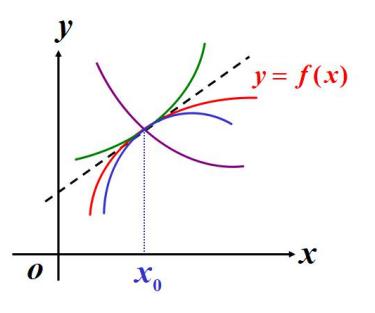
以此类推:
我们所找的多项式应该满足下面条件:
解释一下上面的转换时如何做的,以上面第三行的二阶导数为例:
第一个箭头的转换:将 Pn(x) 求二阶导函数后将 x0 带入,求得 Pn(x0) = 2!a2
第二个箭头的转换:所以 f (x0) = 2! a2,所以 a2 = 1/2! * f (x0)
多项式函数:
上面多项式中的系数 a 可以全部由 f(x) 表示,则得到泰勒多项式为:
上式称为 f(x) 在 x0 处关于 (x – x0) 的 n 阶泰勒多项式。
其中误差为:
因为是用多项式函数去无限逼近给定的函数,所以两者之间肯定存在一丢丢的误差。
麦克劳伦公式为:
近似可得:
麦克劳林多项式在做逼近的时候很有用,它可以帮我们实现一个函数,在 x 轴 [0, 1] 之间符合低次幂的图像,在大于 1 的作用域上符合高次幂的图像,这样便可以更好地拟合某些函数。
这里补充一个知识:0的阶乘为1,0的阶乘等于1是人为规定的。
原因如下:一个正整数的阶乘是所有小于等于该数的正整数的积,并且有0的阶乘为1.简单一点是人为规定的,但是它有道理的,因为阶乘是一个递推定义, n! = n*(n-1)!,那么必然有一个初始值需要认为规定。因为 1!=1,根据 1!=1*0!,所以 0!=1。
那么阶乘到底什么意思呢?
首先这里要问了,为什么要使用泰勒公式呢?
实际应用中,泰勒公式需要阶段,只取有限项,一个函数的有限项的泰勒级数叫做泰勒展开式。泰勒公式的余项可以用来估算这种近似的误差。
泰勒公式最直接的一个应用就是用于计算,计算机一般都是把 sin(x) 进行泰勒展开进行计算的。
泰勒公式还可以把问题简化,比如计算:
代入 sin(x) 的泰勒展示有:
其中 o(x3) 是泰勒公式里面的余项,是高阶无穷小。
下面给出几个常见函数在 x=0 处的泰勒级数,即麦克劳林级数。
下面是几个常见的初等函数的带有佩亚诺余项的麦克劳林公式:
佩亚诺余项为 (x – x0)n 的高阶无穷小:Rn(x) = o[(x – x0)n]
拉格朗日乘子法是用来求条件极值的,或者说拉格朗日乘子法叫拉格朗日数乘法求解条件极值,极值问题有两类,其一,求函数在给定区间上的极值,对自变量没有其他要求,这种极值称为无条件极值。其二,对自变量有一些附加的约束条件限制下的极值,称为条件极值。
下面我们一步一步慢慢来
给个函数: u = f(x, y),如何求其极值点呢?
简单来说直接求它的偏导不就OK了,即:
但是:现在问题难度加大了,如果再加上约束条件呢?限制条件为 v(x, y) = 0
解出 y = y(x) 代入 z 中有:
这说明当 u 的梯度与条件 z = z(x, y) 的法向量共线的时候 u 取得条件极值。
由于一般情况下 v(x, y) 很难求出显式子,所以我们运用银行求导的法则:
于是得到:
显然:
于是我们得到结论: u = f(x, y) 在条件 v(x, y) = 0 作用下的极值点由下述函数的极值点给出,注意到 v(x, y) = 0,极值也相同。
老师的PPT:
下面来解析一下。
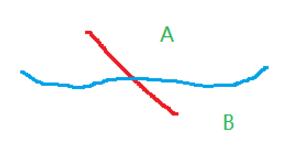
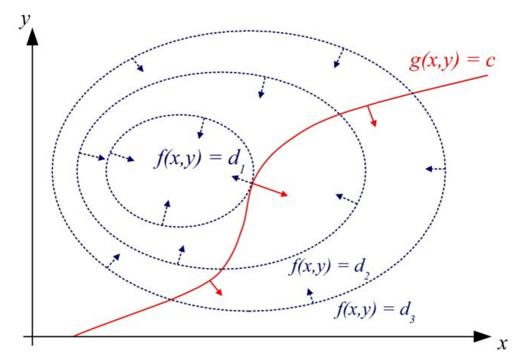
想象一下,目标函数 f (x, y) 是一座山的高度,约束 g(x, y)=C 是镶嵌在山上的一条曲线如上图。为了找到曲线的最低点,就从最低的等高线(0那条)开始往上数。数到第三条,等高线终于和曲线有交点了,如下图所示,因为比这条等高线低的地方都不在约束范围内,所以这肯定是这条约束曲线的最低点了。
而且约束条件在这里不可能和等高线相交,一定是相切。因为如果相交的话,如下图所示,那么曲线肯定会有一部分在B区域,但是B区域比等高线低,这是不可能的。
两条曲线相切,意味着他们在这点的法线(法向量)平行,也就是法向量只差一个任意的常数乘子(取为 – λ)
我们把这个式子的右边移到左边,并把常数移到微分算子,就得到:
把这个式子重新解释一下:这个就是函数 f(x, y) λ g(x, y) 无约束情况下极值点的必要条件。
(上图解释:两曲线相切等价于两曲线在切点处拥有共线的法向量,因此可得到函数 f(x, y) 与 g(x, y)在切线处的梯度(gradient)成正比,于是我们可以列出方程组求解切线的坐标(x,y),进而得到函数 f的极值)
从代数方面再梳理一下:
求一个多元函数 f(x, y, z,…) 在条件 g(x, y, z,….) =a 下的极值,实际上是求前者在后者定义域下的极值。
而求函数 L(r, x, y,z…) = f(x, y, z….) r*(g(x,y,z…)-a) 的无条件极值,极值存在的条件为 L 的所有偏导数等于0。
关键的一点来了,由于 r 也是 L 的变量,所以 L 对 r 的偏导数为 0 相当于要求:
这恰好使 L(r, x, y, z…) 的除了r外的所有变量被限制在 g(x, y, z,…) 的定义域内。
而在这个定义域内,显然 g-a 恒等于0,于是就有 L=f,求 f的有条件极值问题被转化为求 L的无条件极值问题。
在数学最优问题中,拉格朗日乘子法(Lagrange Multiplier,以数学家拉格朗日命名)是一种寻找遍历受一个或多个条件限制的多元函数的极值的方法。
基本的拉格朗日乘子法(又称为拉格朗日乘数法),就是求解函数 f(x1, x2, ….)在 g(x1,x2…)=0的约束条件下的极值的方法。其主要思想是引入一个新的参数 λ (即拉格朗日乘子),将约束条件与原函数联系到一起,使能配成与变量数量相等的等式方程,从而求出得到原函数极值的的各个变量的解。
这种方法将一个有 n 个变量与 k 个约束条件的最优化问题转换为一个有 n k 个变量的方程组的极值问题,其变量不受任何约束。这种方法引入了一种新的标量未知数,即拉格朗日乘数:约束方法的梯度(gradient)的线性组合里每个向量的系数。这种方法保证了在获得最优乘子的情况下,原目标函数的解和拉格朗日函数的解是一致的。
需要注意的是:lagrange函数本身没有意义的,我们只是希望构造出一个 Lagrange函数,来使得这个函数的极值等于原函数 f(x) 在约束条件下的极值。
在机器学习的过程中,我们经常遇到在有限制的情况下,最大化表达式的问题。即求表达式的最大值,一般情况下我们都是求导,令其等于 0,但是机器学习的过程中,我们经常遇到在有限制的情况下,最大化表达式,如下例子所示:
此时,我们引入一个拉格朗日乘子 λ 构造出拉格朗日表达式 :
对于有多个限制的表达式,则有:
其中, λ 称为拉格朗日乘子。
接下来就是要对拉格朗日表达式求导,令其为0,解方程即可。
最后将方程的解代入原函数中即可。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。